Погре́шность измере́ния
— отклонение измеренного значения величины от её истинного (действительного) значения. Погрешность измерения является характеристикой точности измерения.
Выяснить с абсолютной точностью истинное значение измеряемой величины, как правило, невозможно, поэтому невозможно и указать величину отклонения измеренного значения от истинного. Это отклонение принято называть ошибкой измерения
.[1] Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов. На практике вместо истинного значения используют
действительное значение величиных
д, то есть значение физической величины, полученное экспериментальным путём и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него[1]. Такое значение обычно вычисляется как среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому при записи результатов измерений необходимо указывать их точность. Например, запись
T
= 2,8 ± 0,1 с; P = 0,95
означает, что истинное значение величины T
лежит в интервале от
2,7 с
до
2,9 с
с доверительной вероятностью 95 %.
Количественная оценка величины погрешности измерения — мера «сомнения в измеряемой величине» — приводит к такому понятию, как «неопределённость измерения». В то же время иногда, особенно в физике, термин «погрешность измерения» (англ. measurement error) используется как синоним термина «неопределённость измерения» (англ. measurement uncertainty)[2].
Классификация погрешностей измерений
По способу выражения
Абсолютная погрешность[3] Абсолютной погрешностью называют величину, выраженную в единицах измеряемой величины. Её можно описать формулой Δ X = X измеряемый − X истинный . {\displaystyle \Delta X=X_{\text{измеряемый}}-X_{\text{истинный}}.} Вместо истинного значения измеряемой величины на практике пользуются действительным значением X д , {\displaystyle {X_{\text{д}}},} которое достаточно близко к истинному и которое определяется экспериментальным путём и может приниматься вместо истинного. Из-за того что истинное значение величины всегда неизвестно, можно лишь оценить границы, в которых лежит погрешность, с некоторой вероятностью. Такая оценка выполняется методами математической статистики[4]. Относительная погрешность[3] Относительная погрешность выражается отношением δ X = Δ X X д . {\displaystyle \delta X={\frac {\Delta X}{X_{\text{д}}}}.} Относительная погрешность является безразмерной величиной; её численное значение может указываться, например, в процентах.
По источнику возникновения
Инструментальная погрешность[5] Эта погрешность определяется несовершенством прибора, возникающим, например, из-за неточной калибровки. Методическая погрешность[5] Методической называют погрешность, обусловленную несовершенством метода измерений. К таким можно отнести погрешности от неадекватности принятой модели объекта или от неточности расчётных формул. Субъективная погрешность[5] Субъективной является погрешность, обусловленная ограниченными возможностями, ошибками человека при проведении измерений: проявляется, например, в неточностях при отсчёте показаний со шкалы прибора.
По характеру проявления
Случайная погрешность Это составляющая погрешности измерения, изменяющаяся случайным образом в серии повторных измерений одной и той же величины, проведённых в одних и тех же условиях. В появлении таких погрешностей не наблюдается какой-либо закономерности, они обнаруживаются при повторных измерениях одной и той же величины в виде некоторого разброса получаемых результатов. Случайные погрешности неизбежны, всегда присутствуют в результате измерения, однако их влияние обычно можно устранить статистической обработкой. Описание случайных погрешностей возможно только на основе теории случайных процессов и математической статистики.
Математически случайную погрешность, как правило, можно представить белым шумом: как непрерывную случайную величину, симметричную относительно нуля, независимо возникающую в каждом измерении (некоррелированную по времени).
Основным свойством случайной погрешности является то, что искажения искомой величины можно уменьшить путём усреднения данных. Уточнение оценки искомой величины при увеличении количества измерений (повторных экспериментов) означает, что среднее случайной погрешности при увеличении объёма данных стремится к 0 (закон больших чисел).
Часто случайные погрешности возникают из-за одновременного действия многих независимых причин, каждая из которых в отдельности слабо влияет на результат измерения. По этой причине распределение случайной погрешности часто полагают «нормальным» (см. «Центральная предельная теорема»
). «Нормальность» позволяет использовать в обработке данных весь арсенал математической статистики.
Однако априорная убеждённость в «нормальности» на основании центральной предельной теоремы не согласуется с практикой — законы распределения ошибок измерений весьма разнообразны и, как правило, сильно отличаются от нормального.[источник не указан 30 дней
]
Случайные погрешности могут быть связаны с несовершенством приборов (например, с трением в механических приборах), с тряской в городских условиях, с несовершенством самого объекта измерений (например, при измерении диаметра тонкой проволоки, которая может иметь не совсем круглое сечение в результате несовершенства процесса изготовления).
Систематическая погрешность Это погрешность, изменяющаяся по определённому закону (в частности, постоянная погрешность, не изменяющаяся от измерения к измерению). Систематические погрешности могут быть связаны с ошибками приборов (неправильная шкала, калибровка и т. п.), неучтёнными экспериментатором.
Систематическую ошибку нельзя устранить повторными измерениями. Её устраняют либо с помощью поправок, либо «улучшением» эксперимента.
Деление погрешностей на случайные и систематические достаточно условно. Например, ошибка округления при определённых условиях может носить характер как случайной, так и систематической ошибки.
Допустимая погрешность измерений: выбор значения
В.Д. Гвоздев.
Допустимая погрешность измерений: выбор значения
(«Законодательная и прикладная метрология», 2013, №2)
Аннотация
Объектом анализа являются рекомендации по выбору допустимой погрешности измерений, содержащиеся в нормативных документах и публикациях по метрологии. Основное внимание уделено допусковому контролю качества. Подчеркивается, что концепция контроля точности линейных размеров, принятая в ГОСТ 24356, может быть причиной брака.
Ключевые слова:
измерения, контроль, допустимая погрешность измерений, допускаемая погрешность измерений, допуск, оценка соответствия
Для обеспечения единства измерений необходимо, чтобы характеристики погрешности/неопределенности (далее погрешность — Δ) результата измерений не выходили за заданные (допустимые) границы. Методы определения характеристик точности результатов измерений – основная тема метрологии. Выбору значений допустимой погрешности уделяется немного внимания. Часто авторы книг ограничиваются указанием, что выбор допустимой (допускаемой) погрешности производится исходя из задач измерений. Связано это с тем, что в рамках метрологии обосновать выбор значения допустимой погрешности невозможно.
Однако оставить тему выбора допустимой погрешности без рассмотрения также нельзя, хотя бы потому, что при метрологической экспертизе проектов нормативных документов, конструкторской и технологической документации обязательно проверяют оптимальность требований к точности измерений.
Задача измерений – определение значения величины. Цели могут быть разные. Разделим их условно на две группы: 1 — получение информации о величине и 2 — контроль качества объектов.
В первом случае значения допустимой погрешности измерений обусловлены влиянием неопределенности результата измерений на последствия от принятия решения на его основе.
Например:
-если ставится задача повышения точности оценки какой-либо количественной характеристики по отношению к уже достигнутому уровню, допустимая погрешность измерения будет определяться разрядом последней цифры, надежность которой должна быть обеспечена;
-для научных и практических исследований, во многих случаях, допустимую погрешность измерений устанавливают из условия сопоставимости их результатов;
-в медицине точность измерений обусловливается взаимосвязью между изменением параметра и самочувствием пациента;
-в спорте выбор разрешающей способности средств измерений и погрешности измерений связаны с плотностью результатов спортсменов;
-при осуществлении торговых операций с продуктами, характеризуемыми массой или объемом, поставке электроэнергии, тепла, горючих и смазочных материалов и др. от значения допустимой погрешности измерений напрямую зависят экономические показатели поставщика и потребителя;
-при оценке характеристик точности технологических процессов, применении статистических методов контроля технологических процессов, статистическом приемочном контроле и входном контроле качества продукции исходят из критерия ничтожной погрешности измерения по отношению к технологическому допуску. Характеристики точности измерений принимают такими, чтобы среднеквадратическое отклонение (СКО) результата измерений было в 5…6 раз меньше СКО контролируемого параметра [1]. Если СКО контролируемого параметра неизвестно, руководствуются правилом: цена деления не должна превышать 1/6 значения допуска контролируемого параметра [2]. Погрешность измерения в этом случае рассматривают как составную часть погрешности изготовления.
При установлении требований к качеству объектов для значений показателей качества задают односторонние ограничения или двухсторонние ограничения (допуски), которые учитывают при выборе допустимой погрешности измерения. Определим место погрешности измерения при контроле показателя качества с двусторонним ограничением, то есть, когда задан допуск. Обратимся к положению, записанному в стандарте ГОСТ Р ИСО 10576-1-2006 [3]: «решение о соответствии требованиям может быть принято в том случае, если интервал неопределенности результатов измерений находится внутри области допустимых значений». Реализуя принципы оценки соответствия, установленные стандартом, изобразим области соответствия (контролируемый параметр А однозначно находится в заданных пределах) и несоответствия (контролируемый параметр А однозначно находится вне заданных пределов) на числовой оси (рис.).
Рис. Схема измерительного контроля качества отдельного объекта.
Область соответствия 1 определена условием Аmin + Δ ≤ А ≤ Аmax – Δ, области несоответствия 2 (области недопустимых значений) характеризуются неравенствами А ≤ Аmin — Δ и A ≥ Аmax + Δ. Интервалы Аmin ± Δ и Аmax ± Δ назовем областями неокончательного результата оценки соответствия 3. Если истинное значение измеряемой величины находится в области неокончательного результата оценки соответствия, то существует вероятность, что вследствие влияния погрешности измерений годное изделие может быть отнесено к бракованным (неправильно забракованное изделие), а бракованное изделие к годным (неправильно принятое изделие).
При известной функции распределения 4 погрешности измерений можно установить вероятности правильного и неверного решений о соответствии конкретного
изделия.
Применительно к ситуации, показанной на рисунке, если А* истинное значение величины, то Рг — вероятность признания изделия годным, а Рб = 1- Рг — вероятность забракования изделия. Если А* измеренное значение, то Рг — вероятность того, что изделие годное, а Рб — вероятность, что оно бракованное. Достоверность такой информации не высока: сведения о законе распределения случайной погрешности измерений приблизительны или отсутствуют; неисключенные систематические погрешности, рассматриваемые при вычислении суммарной погрешности как случайные величины, в практических измерениях проявляют себя как систематические составляющие, значения и знаки которых неизвестны.
В стандарте [3] не приведены правила для ситуации, когда получен неокончательный результат оценки соответствия. В тоже время о принятия ошибочных решений. Двухэтапная процедура подразумевает повторное выполнение измерений, когда границы интервала неопределенности, рассчитанные после первого этапа, выходят за пределы поля допуска (т.е. результат измерений находится в области неокончательного результата оценки соответствия). Значение измеряемой величины и её неопределенность устанавливают как комбинацию результатов измерений двух этапов.
Для сближения границ области неокончательного результата оценки соответствия применимы меры по уменьшению погрешности измерений, рассмотренные в документе [4].
Границы области соответствия сужаются до нуля при допустимой погрешности измерения равной 0,5 допуска на изготовление и расширяются до границ поля допуска при отсутствии погрешности измерений. Отсюда следует вывод, что значение погрешности измерений при двухстороннем ограничении показателя качества должно быть менее половины значения допуска
и чем оно меньше, тем лучше.
Вывод согласуется с мнением авторов работ [5, 6] и это единственная
общая
рекомендация, которую целесообразно давать в рамках
метрологии
.
В нормативных документах и печатных изданиях по метрологии приводятся другие указания по выбору допустимой погрешности измерений, которые якобы позволяют «достичь необходимой точности изделий с наименьшими затратами труда и материальных средств» [7].
Страница 1 из 3 Следующая
Оценка погрешности при прямых измерениях
При прямых измерениях искомая величина определяется непосредственно по отсчётному устройству (шкале) средства измерения. В общем случае измерения проводятся по определённому методу и при помощи некоторых средств измерений. Эти компоненты несовершенны и вносят свой вклад в погрешность измерения[6]. Если тем или иным путём погрешность измерения (с конкретным знаком) удаётся найти, то она представляет собой поправку, которую просто исключают из результата. Однако достичь абсолютно точного результата измерения невозможно, и всегда остаётся некоторая «неопределённость», которую можно обозначить, оценив границы погрешности[7]. В России методики оценки погрешности при прямых измерениях стандартизированы ГОСТом Р 8.736-2011[8] и Р 50.2.038-2004[9].
В зависимости от имеющихся исходных данных и свойств погрешностей, которые подвергаются оценке, используют различные способы оценки. Случайная погрешность, как правило, подчиняется закону нормального распределения, для нахождения которого необходимо указать математическое ожидание M {\displaystyle M} и среднеквадратическое отклонение σ . {\displaystyle \sigma .} В связи с тем, что при измерении проводится ограниченное число наблюдений, находят только наилучшие оценки этих величин: среднее арифметическое (то есть конечный аналог математического ожидания) результатов наблюдений x ¯ {\displaystyle {\bar {x}}} и среднеквадратическое отклонение среднего арифметического S x ¯ {\displaystyle S_{\bar {x}}} [10][8]:
x ¯ = ∑ i = 1 n x i n {\displaystyle {\bar {x}}={\frac {\sum _{i=1}^{n}x_{i}}{n}}} ; S x ¯ = ∑ i = 1 n ( x i − x ¯ ) 2 n ( n − 1 ) . {\displaystyle S_{\bar {x}}={\sqrt {\frac {\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}}{n(n-1)}}}.}
Доверительные границы ε {\displaystyle \varepsilon } оценки погрешности, полученной таким способом, определяются умножением среднеквадратического отклонения на коэффициент Стьюдента t , {\displaystyle t,} выбранный для заданной доверительной вероятности P : {\displaystyle P:}
ε = t S x ¯ . {\displaystyle \varepsilon =tS_{\bar {x}}.}
Систематические погрешности в силу своего определения не могут быть оценены путём проведения многократных измерений[11]. Для составляющих систематической погрешности, обусловленной несовершенством средств измерений, как правило, известны только их границы, представленные, например, основной погрешностью средства измерения[12].
Итоговая оценка границ погрешности получается суммированием вышеприведённых «элементарных» составляющих, которые рассматриваются как случайные величины. Эта задача может быть математически решена при известных функциях распределений этих случайных величин. Однако в случае систематической погрешности такая функция, как правило, неизвестна и форму распределения этой погрешности задают как равномерную[13]. Основная трудность заключается в необходимости построения многомерного закона распределения суммы погрешностей, что практически невозможно уже при 3—4 составляющих. Поэтому используются приближённые формулы[14].
Суммарную неисключённую систематическую погрешность, когда она состоит из нескольких m {\displaystyle m} компонентов, определяют по следующим формулам[8]:
Θ ∑ = ± ∑ i = 1 m | Θ i | {\displaystyle \Theta _{\sum }=\pm \sum _{i=1}^{m}\left|\Theta _{i}\right|} (если m < 3 {\displaystyle m<3} ); Θ ∑ ( P ) = ± k ∑ i = 1 m Θ i 2 {\displaystyle \Theta _{\sum }(P)=\pm k{\sqrt {\sum _{i=1}^{m}\Theta _{i}^{2}}}} (если m ⩾ 3 {\displaystyle m\geqslant 3} ), где коэффициент k {\displaystyle k} для доверительной вероятности P = 0 , 95 {\displaystyle P=0{,}95} равен 1,1.
Суммарная погрешность измерения, определяемая случайной и систематической составляющей, оценивается как[15][8]:
Δ = K S x ¯ 2 + Θ ∑ 2 3 {\displaystyle \Delta =K{\sqrt {S_{\bar {x}}^{2}+{\frac {\Theta _{\sum }^{2}}{3}}}}} или Δ = K S x ¯ 2 + ( Θ ∑ ( P ) k 3 ) 2 {\displaystyle \Delta =K{\sqrt {S_{\bar {x}}^{2}+\left({\frac {\Theta _{\sum }(P)}{k{\sqrt {3}}}}\right)^{2}}}} , где K = ε + Θ ∑ S x ¯ + Θ ∑ 3 {\displaystyle K={\frac {\varepsilon +\Theta _{\sum }}{S_{\bar {x}}+{\frac {\Theta _{\sum }}{\sqrt {3}}}}}} или K = ε + Θ ∑ ( P ) S x ¯ + Θ ∑ ( P ) k 3 . {\displaystyle K={\frac {\varepsilon +\Theta _{\sum }(P)}{S_{\bar {x}}+{\frac {\Theta _{\sum }(P)}{k{\sqrt {3}}}}}}.}
Окончательный результат измерения записывается как[16][8][17][18] A ± Δ ( P ) , {\displaystyle A\pm \Delta (P),} где A {\displaystyle A} — результат измерения ( x ¯ , {\displaystyle {\bar {x}},} ) Δ {\displaystyle \Delta } — доверительные границы суммарной погрешности, P {\displaystyle P} — доверительная вероятность.
Нормирование погрешностей средств измерений
Нормирование погрешностей средств измерений
Нормирование метрологических характеристик средств измерений и заключается в установлении границ для отклонений реальных значений параметров средств измерений от их номинальных значений.
Каждому средству измерений приписываются некоторые номинальные характеристики. Действительные же характеристики средств измерений не совпадают с номинальными, что и определяет их погрешности.
Обычно нормирующее значение принимают равным:
- большему из пределов измерений, если нулевая отметка расположена на краю или вне диапазона измерения;
- сумме модулей пределов измерения, если нулевая отметка расположена внутри диапазона измерения;
- длине шкалы или её части, соответствующей диапазону измерения, если шкала существенно неравномерна (например, у омметра);
- номинальному значению измеряемой величины, если таковое установлено (например, у частотомера с номинальным значением 50 Гц);
- модулю разности пределов измерений, если принята шкала с условным нулём (например, для температуры), и т.д.
Чаще всего за нормирующее значение принимают верхний предел измерений данного средства измерений.
Отклонения параметров средств измерений от их номинальных значений, вызывающие погрешность измерений, не могут быть указаны однозначно, поэтому для них должны быть установлены предельно допускаемые значения.
Указанное нормирование является гарантией взаимозаменяемости средств измерений.
Нормирование погрешностей средств измерений заключается в установлении предела допускаемой погрешности.
Под этим пределом понимается наибольшая (без учёта знака) погрешность средства измерения, при которой оно может быть признано годным и допущено к применению.
Подход к нормированию погрешностей средств измерений заключается в следующем:
- в качестве норм указывают пределы допускаемых погрешностей, включающие в себя и систематические, и случайные составляющие;
- порознь нормируют все свойства средств измерений, влияющие на их точность.
Стандарт устанавливает ряды пределов допускаемых погрешностей. Этой же цели служит установление классов точности средств измерений.
Классы точности средств измерений
Класс точности – это обобщенная характеристика СИ, выражаемая пределами допускаемых значений его основной и дополнительной погрешностей, а также другими характеристиками, влияющими на точность. Класс точности не является непосредственной оценкой точности измерений, выполняемых этим СИ, поскольку погрешность зависит еще от ряда факторов: метода измерений, условий измерений и т.д. Класс точности лишь позволяет судить о том, в каких пределах находится погрешность СИ данного типа. Общие положения деления средств измерений по классу точности устанавливает ГОСТ 8.401–80.
Пределы допускаемой основной погрешности, определяемые классом точности, – это интервал, в котором находится значение основной погрешности СИ.
Классы точности СИ устанавливаются в стандартах или технических условиях. Средство измерения может иметь два и более класса точности. Например, при наличии у него двух или более диапазонов измерений одной и той же физической величины ему можно присваивать два или более класса точности. Приборы, предназначенные для измерения нескольких физических величин, также могут иметь различные классы точности для каждой измеряемой величины.
Пределы допускаемых основной и дополнительной погрешностей выражают в форме приведенных, относительных или абсолютных погрешностей. Выбор формы представления зависит от характера изменения погрешностей в пределах диапазона измерений, а также от условий применения и назначения СИ.
Пределы допускаемой абсолютной основной погрешности устанавливаются по одной из формул: или , где x – значение измеряемой величины или число делений, отсчитанное по шкале; a, b – положительные числа, не зависящие от х. Первая формула описывает чисто аддитивную погрешность, а вторая – сумму аддитивной и мультипликативной погрешностей.
В технической документации классы точности, установленные в виде абсолютных погрешностей, обозначают, например, «Класс точности М», а на приборе – буквой «М». Для обозначения используются прописные буквы латинского алфавита или римские цифры, причём меньшие пределы погрешностей должны соответствовать буквам, находящимся ближе к началу алфавита, или меньшим цифрам. Пределы допускаемой приведенной основной погрешности определяются по формуле , где xN – нормирующее значение, выраженное в тех же единицах, что и ; p – отвлеченное положительное число, выбираемое из ряда значений:
Нормирующее значение xN устанавливается равным большему из пределов измерений (или модулей) для СИ с равномерной, практически равномерной или степенной шкалой и для измерительных преобразователей, для которых нулевое значение выходного сигнала находится на краю или вне диапазона измерений. Для СИ, шкала которых имеет условный нуль, равно модулю разности пределов измерений.
Для приборов с существенно неравномерной шкалой xN принимают равным всей длине шкалы или ее части, соответствующей диапазону измерении. В этом случае пределы абсолютной погрешности выражают, как и длину шкалы, в единицах длины, а на средстве измерений класс точности условно обозначают, например, в виде значка , где 0,5 – значение числа р (рис. 3.1).
Рис. 3.1.
Лицевая панель фазометра класса точности 0,5 с существенно неравномерной нижней шкалой
В остальных рассмотренных случаях класс точности обозначают конкретным числом р, например 1,5. Обозначение наносится на циферблат, щиток или корпус прибора (рис. 3.2).
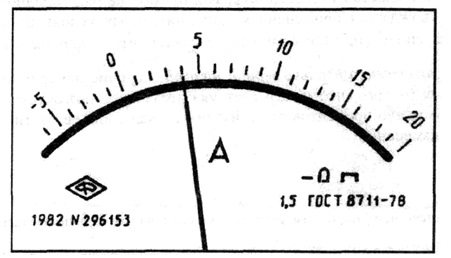
Рис. 3.2.
Лицевая панель амперметра класса точности 1,5 с равномерной шкалой
В том случае если абсолютная погрешность задается формулой , пределы допускаемой относительной основной погрешности
| ( 3.1) |
где с, d – отвлеченные положительные числа, выбираемые из ряда: ; – больший (по модулю) из пределов измерений. При использовании формулы 3.1 класс точности обозначается в виде «0,02/0,01», где числитель – конкретное значение числа с, знаменатель – числа d (рис. 3.3).
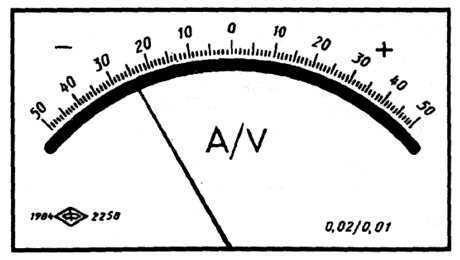
Рис. 3.3.
Лицевая панель ампервольтметра класса точности 0,02/0,01с равномерной шкалой
Пределы допускаемой относительной основной погрешности определяются по формуле , если . Значение постоянного числа q устанавливается так же, как и значение числа p. Класс точности на прибор обозначается в виде , где 0,5 – конкретное значение q (рис. 3.4).
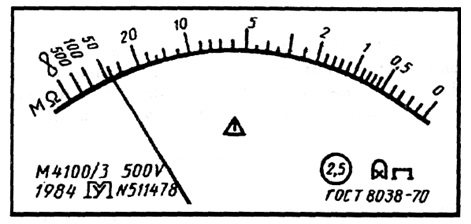
Рис. 3.4.
Лицевая панель мегаомметра класса точности 2,5 с неравномерной шкалой
В стандартах и технических условиях на СИ указывается минимальное значение x0, начиная с которого применим принятый способ выражения пределов допускаемой относительной погрешности. Отношение xk/x0 называется динамическим диапазоном измерения.
Правила построения и примеры обозначения классов точности в документации и на средствах измерений приведены в таблице 3.1.
Таблица 3.1. Обозначение классов точности средств измерений
| Формула для определения пределов допускаемой погрешности | Примеры пределов допускаемой основной погрешности | Обозначение класса точности | |
| В документах | На средствах | ||
| Абсолютная погрешность | |||
| Класс точности М | М | ||
| Класс точности С | С | ||
| Приведенная погрешность | |||
| Класс точности 1,5 | 1,5 | ||
| Класс точности 0,5 | (для СИ с неравномерной шкалой) | ||
| Относительная погрешность | |||
| Класс точности 0,5 | |||
| Класс точности 0,02/0,01 | 0,02/0,01 | ||
Контрольные вопросы
- Поясните, что такое класс точности СИ.
- Является ли класс точности СИ непосредственной оценкой точности измерений, выполняемых этим СИ?
- Перечислите основные принципы, лежащие в основе выбора нормируемых метрологических характеристик средств измерений.
- Как нормируются приборы по классам точности?
- Какие метрологические характеристики описывают погрешность средств измерений?
- Как осуществляется нормирование метрологических характеристик средств измерений?
Погрешность измерения и принцип неопределённости Гейзенберга
Принцип неопределённости Гейзенберга устанавливает предел точности одновременного определения пары наблюдаемых физических величин, характеризующих квантовую систему и описываемых некоммутирующими операторами (например, координаты и импульса, тока и напряжения, электрического и магнитного поля). Таким образом, из аксиом квантовой механики следует принципиальная невозможность одновременного определения с абсолютной точностью некоторых физических величин. Этот факт накладывает серьёзные ограничения на применимость понятия «истинное значение физической величины»[источник не указан 301 день
].
Предельная погрешность измерения и ее составляющие
Общие сведения
ВЫБОР УНИВЕРСАЛЬНЫХ СРЕДСТВ ИЗМЕРЕНИЙ ДЛЯ ОЦЕНКИ ЛИНЕЙНЫХ РАЗМЕРОВ
Погрешности средств измерения (СИ) приводят к тому, что результат измерения не соответствует истинному размеру детали. Из-за погрешностей измерений детали с правильными размерами могут быть ошибочно забракованы и, наоборот, детали с неправильными размерами иногда признаются годными. Попадание на сборку деталей с неправильными размерами приводит к выпуску бракованных изделий и может принести существенный материальный ущерб. Для правильного выбора СИ необходимо уметь оценить влияния погрешностей измерения на результаты контроля.
Влияние погрешностей измерения на результат контроля определяется величиной предельной погрешности измерения. Пределы допустимых погрешностей измерения, в зависимости от допусков на изготовление и номинальных измеряемых размеров, не должны превышать значений, указанных в табл.30 ГОСТ 8.053-81 «Погрешности, допускаемые при измерении линейных размеров до 500 мм».
Табл.30 построена так, что для каждого интервала диаметров (от самого маленького интервала до 3 мм до самого большого 400-500 мм) предусмотрено 16 рядов пределов допускаемых погрешностей измерения: от наиболее точного ряда, соответствующего квалитету 2, до наименее точного — квалитету 17. В каждом ряду приводятся две величины: допуск (IT) на изготовление детали (который берется непосредственно с чертежа контролируемой детали) и допускаемая погрешность измерения (δ).
Принцип выбора средств измерения заключается в сравнении предельной (суммарной) погрешности измерений Δ∑ с табличной допустимой погрешностью измерений δ. Соотношение этих погрешностей для получения результата измерений с погрешностью не более заданной должно быть Δ∑ ≤ δ.
Примечания
- ↑ 12
В ряде источников, например в Большой советской энциклопедии, термины
ошибка измерения
и
погрешность измерения
используются как синонимы, но, согласно рекомендации РМГ 29-99, термин
ошибка измерения
, считающийся менее удачным, не рекомендуется применять, а РМГ 29-2013 его вообще не упоминает. См. «Рекомендации по межгосударственной сертификации 29-2013. ГСИ. Метрология. Основные термины и определения». - Olive K. A. et al. (Particle Data Group).
38. Statistics. — В: 2014 Review of Particle Physics // Chin. Phys. C. — 2014. — Vol. 38. — P. 090001. - ↑ 12
Фридман, 2008, с. 42. - Фридман, 2008, с. 41.
- ↑ 123
Фридман, 2008, с. 43. - Рабинович, 1978, p. 19.
- Рабинович, 1978, p. 22.
- ↑ 1 2 3 4 5
ГОСТ Р 8.736-2011 ГСИ. Измерения прямые многократные. Методы обработки результатов измерений. Основные положения / ВНИИМ. — 2011. - Р 50.2.038-2004 ГСИ. Измерения прямые однократные. Оценивание погрешностей и неопределенности результата измерений.
- Рабинович, 1978, p. 61.
- Фридман, 2008, с. 82.
- Рабинович, 1978, p. 90.
- Рабинович, 1978, p. 91.
- Новицкий, 1991, p. 88.
- Рабинович, 1978, p. 112.
- МИ 1317-2004 ГСИ. Рекомендация. Результаты и характеристики погрешности измерений. Формы представления. Способы использования при испытаниях образцов продукции и контроле их параметров / ВНИИМС. — Москва, 2004. — 53 с.
- Р 50.2.038-2004 Измерения прямые однократные. Оценивание погрешностей и неопределенности результата измерений / ВНИИМ. — 2011. — 11 с.
- ↑ 12
МИ 2083-90 ГСИ. Измерения косвенные определение результатов измерений и оценивание их погрешностей / ВНИИМ. — 11 с. - Фридман, 2008, с. 129.
Литература
- Якушев А. И., Воронцов Л. Н., Федотов Н. М.
Взаимозаменяемость, стандартизация и технические измерения. — 6-е изд., перераб. и доп.. — М.: Машиностроение, 1986. — 352 с. - Гольдин Л. Л., Игошин Ф. Ф., Козел С. М. и др.
Лабораторные занятия по физике. Учебное пособие / под ред. Гольдина Л. Л.. — М.: Наука. Главная редакция физико-математической литературы, 1983. — 704 с. - Назаров Н. Г.
Метрология. Основные понятия и математические модели. — М.: Высшая школа, 2002. — 348 с. — ISBN 5-06-004070-4. - Деденко Л. Г., Керженцев В. В.
Математическая обработка и оформление результатов эксперимента. — М.: МГУ, 1977. — 111 с. — 19 250 экз. - Рабинович С. Г.
Погрешности измерений. — Ленинград, 1978. — 262 с. - Фридман А. Э.
Основы метрологии. Современный курс. — Санкт-Петербург: НПО «Профессионал», 2008. — 284 с. - Новицкий П. В., Зограф И. А.
Оценка погрешностей результатов измерений. — Л.: Энергоатомиздат, 1991. — 304 с. — ISBN 5-283-04513-7.






